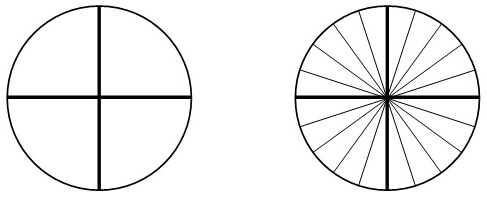Շրջանը բաժանենք 4 հավասար մասերի և նրանցից 3-ը ներկենք, իսկ հետո յուրաքանչյուր քառորդ շրջանը բաժանենք ևս 5 հավասար մասերի: Սյդ դեպքում ամբողջ շրջանը բաժանված կլինի 4 * 5 = 20 մասերի, երեք ներկված քառորդ շրջաններում կլինեն՝ 3 * 5 = 15 այդպիսի մասեր: Ուստի՝

3 4

= 3 * 5 4 * 5 = 15 20 , այսինքն՝ 3 4 = 15 20 :

Այաս հավասարությունը կարելի է գրել այսպես՝

15 20

= 15 : 5 20 : 5 = 3 4 :

Ընդհանրապես, եթե կոտորակի համարիչը և հայտարարը բազմապատկեն կամ բաժանեն միևնույն բնական թվով, ապա կստացվի նրան հավասար կոտորակ: Այս հատկությունն անվանում են կոտորակի հիմնական հատկություն:
Օրինակ՝

2 5

= 4 10 ; 9 15 = 3 5 ; 16 8 = 2 1 :

Երկու հավասար կոտորակները միևնույն թվի տարբեր գրելաձևեր են:
Բնական թվերը, կոտորակային թվերը, ինչպես նաև նրանց հակադիր թվերը և զրոն անվանում են ռացիոնալ թվեր:

Օրինակ՝ 8;

6 7

; - 3 5 ; 12 14 ; - 9 15 ; 0; 0.23; 23 100 ռացիոնալ թվեր են, ընդ

որում

6 7

-ը և 12 14 -ը միևնույն ռացիոնալ թիվն է: Ճիշտ այդպես էլ

հավասար են 8 և

24 3

թվերը, - 3 5 և - 9 15 -ը, 0.23-ը և 23 100 -ը:

Եթե բաժանելին և բաժանարարը ամբողջ թվեր են, ընդ որում բաժանարարը հավասար չէ զրոյի, ապա քանորդը ռացիոնալ թիվ է՝

-3 : 4 = - (3 : 4) =

- 3 4

; -3 : (-4) = 3 : 4 = 3 4 :

Հետագայում մենք կոտորակ կանվանենք ցանկացած a/b տեսքի արտահայտություն, որտեղ a-ն և b-ն ամբողջ թվեր են և a ≠ 0, b ≠ 0: Յուրաքանչյուր այդպիսի կոտորակ նշանակում է որևէ ռացիոնալ թիվ:

Օրինակ՝

-3 4

= - 3 4 ; -5 -8 = 5 8 ; 4 -9 = - 4 9 :