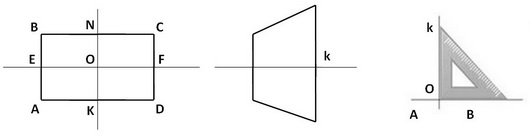ABCD ուղղանկյան AB և CD կողմերի E և F միջնակետերով տանենք EF ուղիղը: Այդ ուղիղը կիսում է ուղղանկյունը: Այդ ուղղով ժալելով ուղղանկյունը, նրա երկու մասերը համընկնում են: Ասում են, որ ուղղանկյունը համաչափ է EF ուղղի նկատմամբ, իսկ EF ուղիղն անվանում են ուղղանկյան համաչափության առանցք: ABCD ուղղանկյունն ունի ևս մեկ համաչափության առանցքը՝ NK ուղղիղը:
Ընդհանրապես, պատկերն անվանում են k ուղղի նկատմամբ համաչափ, եթե այդ ուղիղը կիսում է պատկերը երկու մասերի, որոնք համընկնում են այդ ուղղով ծալելիս: k ուղիղն անվանում են այդ պատկերի համաչափության առանցք:
A և B երկու կետեր, որոնք համընկնում են հարթությունը k ուղղով ծալելու դեպքում, անվանում են համաչափ այդ ուղղի նկատմամբ: Եթե A և B կետերը համաչափ են k ուղղի նկատմամբ, ապա. 1) AB հատվածն ուղղահայաց է k ուղղին, 2) k ուղիղը կիսում է այդ հատվածը: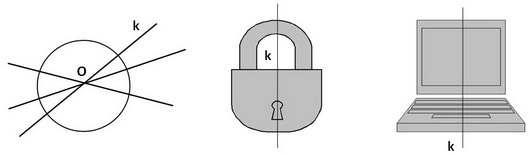Շրջանագիծն ունի անվերջ թվով համաչափության առանցքներ՝ ցանկացած ուղիղ, որն անցնում է շրջանագծի կենտրոնով, նրա համաչափության առանցքն է:
Համաչափության առանցք ունեն նաև բնության մեջ և տեխնիկայում հաճախ հանդիպող շատ պատկերներ (առարկաներ):