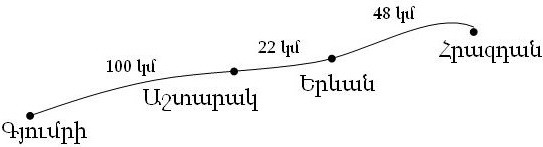Երևան քաղաքը գտնվում է Հրազդանի և Աշտարակի միջև: Հրազդանից մինչև Երևան 48 կմ է, իսկ Երևանից մինչև Աշտարակ` 22 կմ: Ուստի Հրազդանից մինչև Աշտարակ հեռավորությունը հավասար է 48 + 22 կմ: Եթե մենք գնանք Աշտարակից Հրազդան, ապա մինչև Երևան կանցնենք 22 կմ, իսկ հետո` Երևանից մինչև Հրազդան, ևս 48 կմ: Ընդամենը մենք կանցնենք 22 + 48 կմ: Բայց Հրազդանից մինչև Աշտարակ հեռավորությունը նույնն է, ինչ Աշտարակից մինչև Հրազդան: Ուստի48 + 22 = 22 + 48Ընդհանրապես, a-ի և b-ի ցանկացած արժեքների դեպքում ճիշտ էa + b = b + aհավասարությունը:
Գումարման այս հատկությունն անվանում են գումարման տեղափոխական օրենք: Այն կարդում են այսպես` գումարելիների տեղափոխությունից գումարի արժեքը չի փոխվում:
Աշտարակ և Երևան քաղաքները գտնվում են Գյումրի և Հրազդան քաղաքների միջև: Եթե մենք գնանք Հրազդանից Գյումրի, կանգ առնելով միայն Աշտարակում, ապա կանցնենք նախ 48 + 22 կմ, հետո էլի 100 կմ: Ընդամենը ստացվում է (48 + 22) + 100 կմ: Իսկ եթե գնանք Հրազդանից Գյումրի, կանգ առնելով միայն Երևանում, ապա կանցնենք նախ 48 կմ, հետո էլի 22 + 100 կմ: Ստացվում է ընդամենը 48 + (22 + 100) կմ: Քանի որ երկու դեպքում էլ մենք անցել ենք միևնույն հեռավորությունը, ապա(48 + 22) + 100 = 48 + (22 + 100) Ընդհանրապես, a-ի, b-ի և c-ի ցանկացած արժեքների դեպքում ճիշտ է հետևյալ հավասարությունը(a + b) + c = a + (b + c)Գումարման այս հատկությունն անվանում են գումարման զուգորդական օրենք: Այն կարդում են այսպես` երկու թվերի գումարին երրորդ թիվն ավելացնելու համար կարելի է առաջին թվին ավելացնել երկրորդի և երրորդի գումարը:
Պայմանավորվել են (a + b) + c արտահայտությունը գրել առանց փակագծերի.a + b + c Նշենք զրոյի հատկությունը գումարելիս. եթե երկու գումարելիներից մեկը հավասար է զրոյի, ապա գումարը հավասար է մյուս գումարելիին:
a–ի ցանկացած արժեքների դեպքում ճիշտ ենa + 0 = a և 0 + a = a հավասարությունները: