Դիտարկենք գծային հավասարումների համակարգի լուծման ևս մեկ եղանակ՝ գումարման եղանակը: Համակարգը այդ եղանակով լուծելիս, ինչպես որ տեղադրման եղանակով լուծելիս, մենք տվյալ համակարգից անցնում ենք մեկ այլ՝ համարժեք համակարգի, որի մեջ հավասարումներից մեկը պարունակում է միայն մեկ փոփոխական:
Օրինակ 1: Լուծենք հավասարումների համակարգը.

{	2x + 3y = -5,
	x – 3y = 38:                    (1)

Այս համակարգի հավասարումներում y-ի գործակիցները հակադիր թվեր են: Անդամ առ անդամ գումարելով հավասարումների աջ և ձախ մասերը, կստանանք մեկ փոփոխականով հավասարում.3x = 33:(1) համակարգի հավասարումներից մեկը. օրինակ՝ առաջինը, փոխարինենք 3x = 33 հավասարմամբ: Կստանանք այս համակարգը.

{	3x = 33,
	x – 3y = 38:                    (2)

(2) համակարգը համարժեք է (1) համակարգին: Դրանում կարելի է համոզվել այնպիսի դատողությունների օգնությամբ, որոնք նման են նախորդ կետում մեջբերված դատողություններին՝ համակարգը տեղադրման եղանակով լուծելիս:
Լուծենք (2) համակարգը: 3x = 33 հավասարումից գտնում ենք, որ x = 11: x-ի այդ արժեքը տեղադրելով x – 3y = 38 հավասարման մեջ, ստանում ենք հավասարում y փոփոխականով.11 – 3y = 38:Լուծենք այդ հավասարումը.-3y = 27,
y = -9:(11, -9) զույգը (2) համակարգի լուծումն է, և նշանակում է՝ լուծում է նաև տվյալ (1) համակարգի:
Օգտվելով այն բանից, որ (1) համակարգի հավասարումներում y-ի գործակիցները հակադիր թվեր են, մենք նրա լուծումը հանգեցրինք համարժեք (2) համակարգի լուծմանը, որի մեջ հավասարումներից մեկը պարունակում է միայն մեկ փոփոխական:
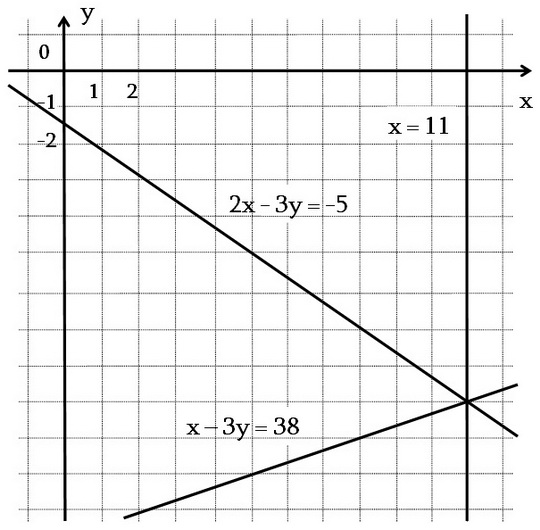
(1) և (2) համակարգերի համարժեքությունը երկրաչափորեն նշանակում է, որ 2x + 3y = -5 և x – 3y = 38 հավասարումների գրաֆիկները հատվում են այն նույն կետում, ինչ որ 3x = 33 և x – 3y = 38 հավասարումների գրաֆիկները, այսինքն բոլոր երեք ուղիղներն էլ հատվում են մեկ կետում:

Օրինակ 2: Լուծենք համակարգը.

{	5x + 11y = 8,
	10x – 7y = 74:

Համակարգի հավասարումների անդամ առ անդամ գումարումը չի հանգեցնում փոփոխականներից մեկի արտաքսման: Սակայն եթե առաջին հավասարման բոլոր անդամները բազմապատկենք -2-ով, իսկ երկրորդ հավասարումը թողնենք անփոփոխ, ապա ստացված հավասարումներում x-ի գործակիցները կդառնան հակադիր թվեր:

{	-10x – 22y = -16,
	10x – 7y = 74:

Այժմ անդամ առ անդամ գումարումը հանգեցնում է մեկ փոփոխականով հավասարման՝ -29y = 58: Այդ հավասարումից գտնում ենք, որ y = -2: Երկրորդ հավասարման մեջ y-ի փոխարեն տեղադրելով -2 թիվը կգտնենք x-ի արժեքը.10x – 7 * (-2) = 74,
10x = 60,
x = 6:Պատասխան. x = 6, y = -2:
Օրինակ 3: Լուծենք հավասարումների համակարգը.

{	3x – 5y = 93,
	5x – 4y = 103:

Համակարգի հավասարումների համար ընտրենք այնպիսի բազմապատկիչներ, որպեսզի դրանցով բազմապատկելուց հետո y-ի գործակիցները դառնան հակադիր թվեր: Համակարգի առաջին հավասարումը բազմապատկելով -4-ով, իսկ երկրորդը՝ 5-ով, կստանանք՝

{	-12x + 20y = -372,
	25x – 20y = 515:

Այստեղից կգտնենք, որ13x = 143,
x = 11:x-ի արժեքը տեղադրելով 5x – 4y = 103 հավասարման մեջ, գտնում ենք, որ y = -12:
Պատասխան. x = 11, y = -12:
Մենք դիտարկեցինք համակարգերի լուծման օրինակներ՝ գումարման եղանակով: Երկու փոփոխականով երկու գծային հավասարումների համակարգը գումարման եղանակով լուծելիս՝ վարվում են հետևյալ կերպ.

1) համակարգի հավասարումները անդամ առ անդամ բազմապատկում են՝ բազմապատկիչներն այնպես ընտրելով, որ փոփոխականներից մեկի գործակիցները դառնան հակադիր թվեր,
2) անդամ առ անդամ գումարում են համակարգի հավասարումների աջ և ձախ մասերը,
3) լուծում են ստացված մեկ փոփոխականով հավասարումը,
4) գտնում են երկրորդ փոփոխականի համապատասխան արժեքը:

Նշենք, որ եթե փոփոխականներից մեկի գործակիցները հակադիր թվեր են, ապա լուծումը միանգամից սկսում են հավասարումներն անդամ առ անդամ գումարելուց: