Դիտարկենք երկու փոփոխականով գծային հավասարումների համակարգերի լուծման մի եղանակ, որը կոչվում է տեղադրման եղանակ: Սկսենք օրինակի դիտարկումից:
Օրինակ 1: Լուծենք հավասարումների համակարգը.

{	3x + y = 7,
	-5x + 2y = 3:                    (1)

Առաջին հավասարման մեջ y-ն արտահայտենք x-ի միջոցով.y = 7 – 3x:Երկրորդ հավասարման մեջ y-ի փոխարեն տեղադրելով 7 – 3x արտահայտությունը կստանանք այս համակարգը.

{	3x + y = 7,
	-5x + 2 (7 – 3x) = 3:                    (2)

(1) և (2) համակարգերն ունեն միևնույն լուծումը:
Ապացուցենք դա: Դիցուք որևէ (a; b) թվազույգ (1) համակարգի լուծումն է: Այդ դեպքում ճիշտ են 3a + b = 7 և -5a + 2b = 3 թվային հավասարությունները, և նշանակում է՝ նաև b = 7 – 3a հավասարությունը: -5a + 2b = 3 հավասարման մեջ b թիվը փոխարինելով 7 – 3a արտահայտությամբ՝ որի արժեքը հավասար է b-ի, մենք նորից կստանանք թվային ճիշտ հավասարություն՝-5a + 2 (7 – 3a) = 3:Նշանակում է (1) համակարգի յուրաքանչյուր լուծում լուծում է նաև (2) համակարգի համար:
Համանման կերպով ապացուցվում է, որ (2) համակարգի յուրաքանչյուր լուծում լուծում է նաև (1) համակարգի համար:
(2) համակարգի մեջ երկրորդ հավասարումը պարունակում է միայն մեկ փոփոխական: Լուծենք այդ հավասարումը.-5x + 14 – 6x = 3,
-11x = -11,
x = 1:y = 7 – 3x հավասարության մեջ x-ի մեջ տեղադրելով 1 թիվը, գտնենք y-ի համապատասխան արժեքը.y = 7 – 3 * 1,
y = 4:(1; 4) զույգը (2) համակարգի լուծում է. նշանակում է՝ լուծում է նաև տվյալ (1) համակարգի համար:
(1) համակարգի լուծումը մենք հանգեցրինք (2) համակարգի լուծմանը: Ընդ որում մենք օգտվեցինք այն բանից, որ (1) և (2) համակարգերը ունեն միևնույն լուծումները:
Երկու փոփոխականով հավասարումների այն համակարգերը, որոնք ունեն միևնույն լուծումները, կոչվում են համարժեք: Լուծումներ չունեցող համակարգերը նույնպես համարվում են համարժեք:
(1) և (2) համակարգերի համարժեքությունը երկրաչափորեն նշանակում է, որ (1) համակարգի հավասարումների գրաֆիկները հատվում են այն նույն կետում, ինչ (2) համակարգի հավասարումների գրաֆիկները, այսինքն բոլոր երեք ուղիղներն էլ հատվում են մի կետում:

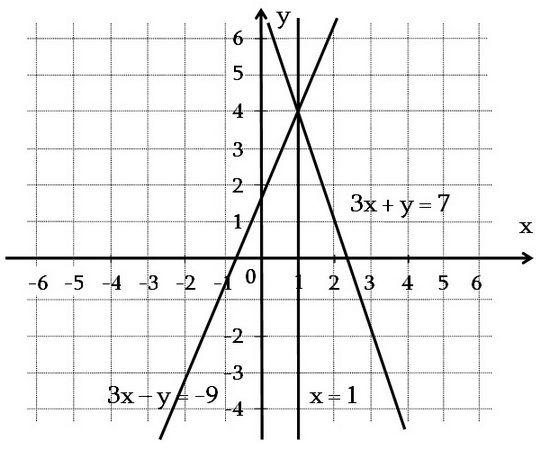Մենք (1) համակարգը լուծեցինք օգտագործելով տեղադրման եղանակը: Երկու փոփոխականով երկու գծային հավասարումների համակարգը տեղադրման եղանակով լուծելիս վարվում են հետևյալ կերպ.

1) համակարգի որևէ հավասարման մեջ մի փոփոխականը արտահայտում են մյուսով,
2) համակարգի մյուս հավասարման մեջ այդ փոփոխականի փոխարեն տեղադրում են ստացված արտահայտությունը,
3) լուծում են ստացված մեկ փոփոխականով հավասարումը,
4) գտնում են երկրորդ փոփոխականի համապատասխան արժեքը:

Օրինակ 2: Լուծենք հավասարումների համակարգը.

{	7x + 6y = 6,
	3x + 4y = 9:

Երկրորդ հավասարման մեջ x-ը արտահայտենք y-ի միջոցով.3x = 9 – 4y,

x =

9 - 4y 3

:

Առաջին հավասարման մեջ x-ի փոխարեն տեղադրենք համարժեք արտահայտությունը.

7 *

9 - 4y 3

+ 6y = 6:

Լուծենք y փոփոխականով ստացված հավասարումը.7 (9 – 4y) + 3 * 6y = 3 * 6y,
63 – 28y + 18y = 18,
-10y = -45, y = 4.5:Օգտագործելով y-ի արժեքը կստանանք՝

x =

9 - 4 * 4.5 3

, x = -3:

Պատասխան: x = -3, y = 4.5: