Խնդիր: Երկու թվերի `գումարը հավասար է 12-ի, իսկ տարբերությունը՝ 2-ի: Գտեք այդ թվերը:
Առաջին թիվը նշանակենք x տառով, իսկ երկրորդը՝ y տառով: Ըստ խնդրի պայմանի թվերի գումարը հավասար է 12-ի, այսինքն՝x + y = 12:Քանի որ թվերի տարբերությունը հավասար է 2-ի, ապա՝x - y = 2:Մենք կազմեցինք երկու հավասարում՝ երկու փոփոխականով: Խնդրի հարցին պատասխանելու համար պետք է գտնել փոփոխականների այնպիսի արժեքներ, որոնք ճշմարիտ հավասարություն են դարձնում x + y = 12 և x – y = 2 հավասարումներից յուրաքանչյուրը, այսինքն գտնել այդ հավասարումների ընդհանուր լուծումը: Այդպիսի դեպքերում ասում են, որ պահանջվում է լուծել հավասարումների համակարգը:
Հավասարումների համակարգը ընդունված է գրառել մեծ փակագծերի միջոցով: Հավասարումների այդ համակարգը կարելի է գրել այսպես.

{	x + y = 12,
	x – y = 2:

Փոփոխականների x = 7, y = 5 արժեքների զույգը համակարգի յուրաքանչյուր հավասարման համար լուծում է, քանի որ 7 + 5 = 12 և 7 – 5 = 2 երկու հավասարումն էլ ճշմարիտ են: Այդպիսի զույգը անվանում են համակարգի լուծում:
Սահմանում: Երկու փոփոխականով հավասարումների համակարգի լուծում կոչվում է փոփոխականների արժեքների այն զույգը, որը համակարգի յուրաքանչյուր հավասարում վերածում է ճշմարիտ հավասարության:
Լուծել հավասարումների համակարգը՝ նշանակում է գտնել նրա լուծումները կամ ապացուցել, որ լուծումներ չկան:
Երկու փոփոխականով գծային հավասարումների համակարգը լուծելու համար կարելի է օգտագործել հավասարումների գրաֆիկները:
Դիցուք պահանջվում է լուծել հավասարումների հետևյալ համակարգը՝

{	2x + 3y = 5,
	3x – y = -9:

Կոորդինատային հարթության մեջ կառուցենք համակարգի հավասարումների գրաֆիկները: Առաջին հավասարման գրաֆիկը AB ուղիղն է, իսկ երկրորդ հավասարմանը՝ CD ուղիղը:

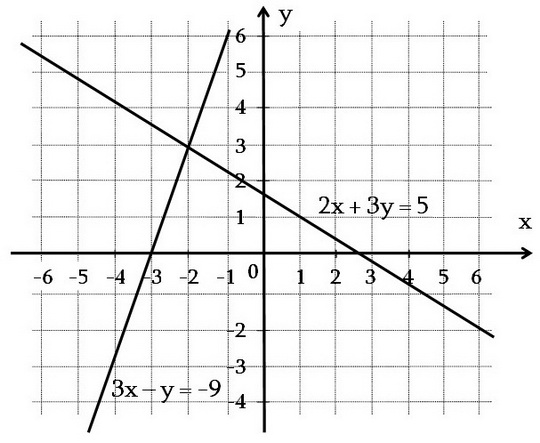AB ուղղի ցանկացած կետի կոորդինատներ 2x + 3y = 5 հավասարման լուծում են, իսկ CD ուղղի ցանկացած կետի կոորդինատներ լուծում են 3x – y = -9 հավասարման համար: Ուղիղների հատման կետի կոորդինատները բավարարում են ինչպես առաջին հավասարմանը, այնպես էլ՝ երկրորդ, այսինքն համակարգի լուծում են: Գրաֆիկները հատվում են k(-2; 3) կետում: Նշանակում է համակարգն ունի միակ լուծում՝ x = -2, y = 3:
Հավասարումների համակարգի լուծման մեր կիրառած եղանակը կոչվում է գրաֆիկական: Նշենք, որ գրաֆիկական եղանակով սովորաբար հնարավոր է գտնել լոկ մոտավոր լուծումը:
Դիտարկենք երկու փոփոխականներով երկու գծային հավասարումների համակարգեր, որոնցից յուրաքանչյուրի մեջ փոփոխականների գործակիցներից գոնե մեկը հավասար չէ զրոյի: Պարզենք, թե արդյո՞ք այդպիսի համակարգը միշտ լուծում ունի և եթե ունի՝ ապա քանիսը: Համակարգի հավասարումների գրաֆիկները ուղիղներ են: Եթե այդ ուղիղները հատվում են, ապա համակարգն ունի միակ լուծում, եթե ուղիղները զուգահեռ են, ապա համակարգը լուծում չունի, եթե ուղիղները համընկնում են, ապա կան անթիվ լուծումներ:
Օրինակ 1: Պարզենք, թե քանի՞ լուծում ունի հավասարումների համակարգը.

{	11x + 10y = 120,
	6x + y = 18:

Դիտարկենք, թե ինչպիսին է տվյալ համակարգի հավասարումների գրաֆիկների փոխադարձ դիրքը: Դրա համար յուրաքանչյուր հավասարման մեջ y-ն արտահայտենք x-ի միջոցով, կստանանք՝

{	y = -1.1x + 12,
	y = -6x + 18:

y = 1.1x + 12 և y = -6x + 18 հավասարումներով տրվում են գծային ֆունկցիաներ: Այդ ֆունկցիաների գրաֆիկներ հանդիսացող ուղիղների անկյունային գործակիցները տարբեր են: Նշանակում է, այդ ուղիղները հատվում են և համակարգն ունի միակ լուծում:
Օրինակ 2: Քննարկենք, թե քանի՞ լուծում ունի հավասարումների համակարգը.

{	8x + 20y = 3,
	2x + 5y = 16:

Համակարգի յուրաքանչյուր հավասարման մեջ y-ն արտահայտենք x-ի միջոցով.

{	y = -0.4x + 0.15,
	y = -0.4x + 3.2:

y = -0.4x + 0.15 և y = -0.4x + 3.2 գծային ֆունկցիաների գրաֆիկներ հանդիսացող ուղիղները զուգահեռ են, քանի որ նրանց անկյունային գործակիցները նույնն են, իսկ y առանցքի հետ հատման կետերը՝ տարբեր: Այստեղից հետևում է, որ հավասարումների տվյալ համակարգը լուծում չունի:
Օրինակ 3: Պարզենք, թե քանի՞ լուծում ունի հավասարումների համակարգը.

{	5x + 2y = -18,
	15x + 6y = -54:

Համակարգի յուրաքանչյուր հավասարման մեջ y-ն արտահայտելով x-ի միջոցով, կստանանք.

{	y = -2.5x - 9,
	y = -2.5x - 9:

Ակնհայտ է, որ հավասարումների գրաֆիկները համընկնում են: Դա նշանակում է, որ (x; y) ցանկացած թվազույգ, որտեղ x-ը կամայական թիվ է, իսկ y = -2.5x – 9, այդ հավասարման լուծում է: Համակարգն ունի անվերջ շատ լուծումներ: