Թվերի յուրաքանչյուր զույգ, որը x և y փոփոխականներով հավասարման լուծում է, կոորդինատային հարթության մեջ պատկերվում է մի կետով, որի կոորդինատները այդ թվազույգն է (աբսցիսը x-ի արժեքն է, իսկ օրդինատը՝ y-ի արժեքը): Նման բոլոր կետերից բաղկանում է հավասարման գրաֆիկը:
Երկու փոփոխականներով հավասարման գրաֆիկ է կոչվում կոորդինատայի հարթության այն բոլոր կետերի բազմությունը, որոնց կոորդինատները այդ հավասարման համար լուծում են:
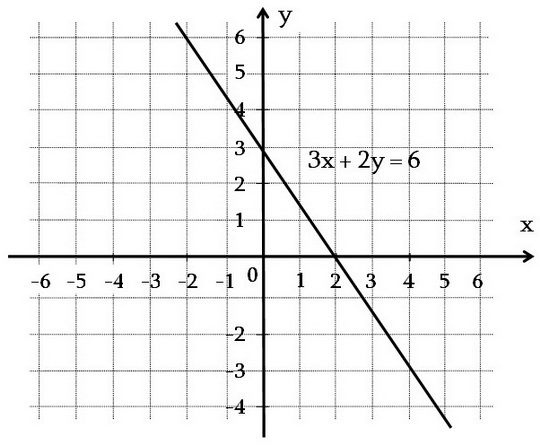
Պարզենք, թե իրենից ինչ է ներկայացնում 3x + 2y = 6 հավասարման գրաֆիկը:
y փոփոխականն արտահայտենք x-ի միջոցով.y = -1.5x + 3:y = -1.5x + 3 բանաձևով տրվում է մի գծային ֆունկցիա, որի գրաֆիկը ուղիղ է: Քանի որ 3x + 2y = 6 և y = -1.5x + 3 հավասարումները համարժեք են, ապա այդ ուղիղը նաև 3x + 2y = 6 հավասարման գրաֆիկն է:

Համանման դատողությունների միջոցով կարելի է ցույց տալ, որ x և y փոփոխականներով ցանկացած գծային հավասարման գրաֆիկ՝ որտեղ y-ի գործակիցը հավասար չէ զրոյի, ուղիղ է:
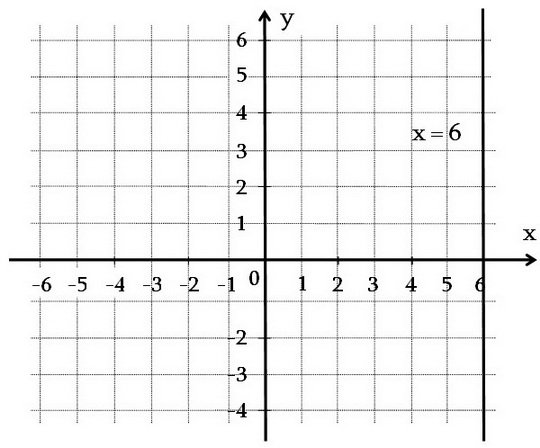
Եթե գծային հավասարման մեջ y-ի գործակիցը հավասար է զրոյի, իսկ x-ի գործակիցը զրոյից տարբեր է, ապա այդպիսի հավասարման գրաֆիկը նույնպես ուղիղ է: Դիտարկենք, օրինակ, 2x + 0y = 12 հավասարումը: Նրա համար լուծում են բոլոր այն (x; y) թվազույգերը, որոնց մեջ x = 6, իսկ y-ը ցանկացած թիվ է, օրինակ (6; 2), (6; 0), (6; -4): Հավասարման գրաֆիկը բաղկացած է բոլոր այն կետերից, որոնց աբսցիսները հավասար են 6-ի, իսկ օրդինատները կամայական թվեր են: Այդպիսի կետերից բաղկանում է մի ուղիղ, որն անցնում է (6; 0) կետով և զուգահեռ է y առանցքին:

Եվ այսպես՝ երկու փոփոխականով գծային հավասարման գրաֆիկը՝ որի մեջ փոփոխականներից գոնե մեկի գործակիցը հավասար չէ զրոյի, ուղիղ է:
Այժմ դիտարկենք այն դեպքը, երբ գծային հավասարման մեջ փոփոխականների երկու գործոկիցներն էլ հավասար են զրոյի:
ax + by = c հավասարումը, որի մեջ երկու փոփոխականների գործակիցներն էլ հավասար են զրոյի, ունի 0x + 0y = c տեսքը: c = 0 դեպքում զանկացած թվազույգ այդ հավասարման արմատ է, իսկ նրա գրաֆիկը ամբողջ կոորդինատային հաևթությունն է: c ≠ 0 դեպքում հավասարումը լուծում չունի և նրա գրաֆիկը ոչ մի կետ չի պարունակում:
Բերենք գծային հավասարումների գրաֆիկների կառուցման օրինակներ:
Օրինակ 1: Կառուցենք 3x – 4y = 12 հավասարման գրաֆիկը:
3x – 4y = 12 հավասարման մեջ փոփոխականների գործակիցները զրոյից տարբեր են: Ուստի նրա գրաֆիկը ուղիղ է: Ուղիղը որոշվում է երկու կետով: Գտնենք այդ ուղղի որևէ երկու կետի կոորդինատներ.
եթե x = 0, ապա y = -3, եթե x = 2, ապա y = -1.5:
Նշենք (0; -3) ու (2; -1.5) կետերը և նրանցով տանենք ուղիղ:

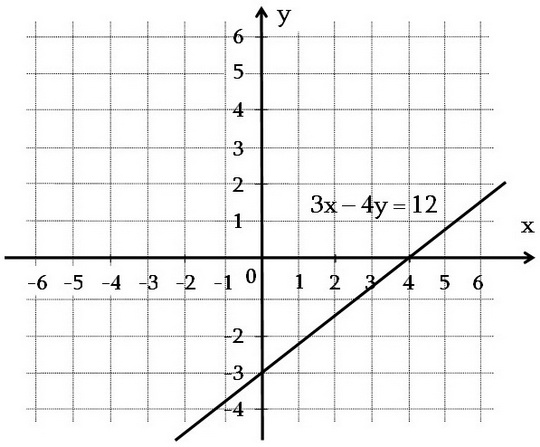Այդ ուղիղը 3x – 4y = 12 հավասարման գրաֆիկն է:
Օրինակ 2: Կառուցենք 0.5x = -1.5 հավասարման գրաֆիկը:
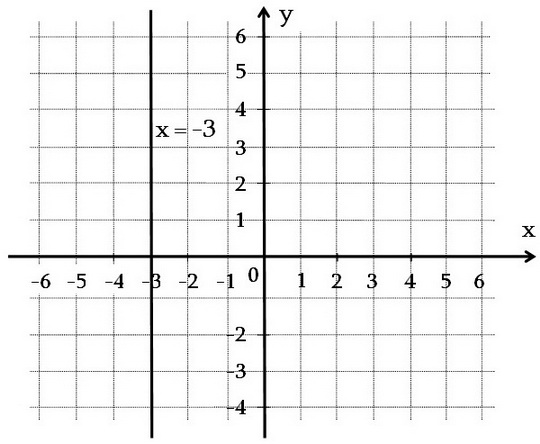
Այդ հավասարումը կարելի է գրել 0.5x + 0y = -1.5 տեսքով: Նրա համար լուծում են այն թվազույգերը, որտեղ x = -3, իսկ y-ը կամայական թիվ է: Հավասարման գրաֆիկը մի ուղիղ է, որն անցնում է (-3; 0) կետով և զուգահեռ է y առանցքին: