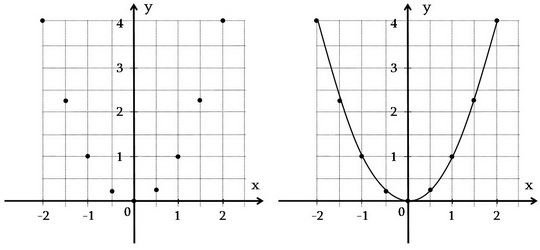y = x² ֆունկցիայի գրաֆիկի միջոցով գտնենք ֆունկցիայի մոտավոր արժեքները, երբ x = 1.5 և x = 2.1:եթե x = 1.5, ապա y ≈ 2.3,
եթե x = 2.1, ապա y ≈ 4.4: y = x² բանաձևով հնարավոր է գտնել այդ ֆունկցիայի ճշգրիտ արժեքները.եթե x = 1.5, ապա y = 1.5² = 2.25,
եթե x = 2.1, ապա y = 2.1² = 4.41:Առաջին օրինակում մոտավոր արժեքները տարբերվում են ճշգրիտ արժեքներից 0.05-ով, իսկ երկրորդում՝ 0.01-ով, քանի որ՝2.3 – 2.25 = 0.05 և 4.41 – 4.4 = 0.01:Իմանալու համար, թե մոտավոր արժեքները որքանով են տարբերվում ճշգրիտ արժեքներից, անհրաժեշտ է մեծ թվից հանել փոքրը: Այլ կերպ ասած՝ պետք է գտնել ճշգրիտ և մոտավոր արժեքների տարբերության բացարձակ մեծությունը: Այդ մեծությունը անվանում են բացարձակ սխալ
Սահմանում: Մոտավոր արժեքի բացարձակ սխալ են անվանում ճշգրիտ և մոտավոր արժեքների տարբերության բացարձակ արժեքը:
Այսպես՝ դիտարկված օրինակում 2.3-ի հավասար մոտավոր արժեքի բացարձակ սխալը հավասար է 0.05-ի, իսկ 4.4-ի հավասար մոտավոր արժեքի բացարձակ սխալը հավասար է 0.01-ի.|2.25 – 2.3| = |-0.05| = 0.05, և |4.41 – 4.4| = 0.01:Միշտ չէ, որ հնարավոր է գտնել բացարձակ սխալը:

Դիցուք, օրինակ, նկարում պատկերված AB հատվածը չափելիս ստացել են հետևյալ արդյունքը.AB ≈ 4.3սմ:Մենք չենք կարող գտնել մոտավոր արժեքի բացարձակ սխալը, քանի որ ճշգրիտ չգիտենք AB հատվածի երկարությունը: Այդպիսի դեպքերում կարևոր է նշել մի այնպիսի թիվ, որից բացարձակ սխալը ավելի մեծ չի կարող լինել: Դիտարկվող օրինակում որպես այդպիսի թիվ կարելի է վերցնել 0.1-ը: Իրոք՝ քանոնի բաժանումների արժեքները 0.1 սանտիմետր են, այդ պատճառով 4.3-ի հավասար մոտավոր արժեքի բացարձակ սխալը մեծ չէ 0.01-ից, այսինքն՝|AB – 4.3| ≤ 0.1:Այդպիսի դեպքերում ասում են, որ 4.3 թիվը AB հատվածի երկարության (սանտիմետրերով) մոտավոր արժեքն է 0.1-ի ճշտությամբ:
Ընդհանրապես՝ եթե x ≈ a և այդ մոտավոր արժեքի բացարձակ սխալը չի գերազանցում որևէ h թվի, ապա a թիվն անվանում են x-ի մոտավոր արժեք h ճշտությամբ: Գրում են՝x ≈ a մինչև h ճշտությամբ:Մոտավոր արժեքի ճշտությունը կախված է շատ պատճառներից: Մասնավորաբար, եթե մոտավոր արժեքը ստացվել է չափելիս, ապա նրա արժեքը կախված է այն սարքից, որի միջոցով կատարել են չափումը: Օրինակ՝ բժշկական ջերմաչափի վրա բաժանումներն արված են 0.1° միջակայքով: Դա հնարավորություն է ընձեռում ջերմաստիճանը չափել մինչև 0.1° ճշտությամբ: Սենյակի ջերմաչափը, որի բաժանումներն արված են 1° միջակայքով, հնարավորություն է ընձեռում ջերմաստիճանը չափել մինչև 1° ճշտությամբ: Առևտրային կշեռքներով, որոնց բաժանումների արժեքը 5 գրամ է, հնարավոր է կշռել մինչև 5գ ճշտությամբ:
Տասնորդական կոտորակները մինչև տասնավորներ, հարյուրավորներ, հազարավորներ և այլն կլորացնելիս ստացվում են մոտավոր արժեքներ 0.1, 0.01, 0.001 և այլն ճշտությամբ: Օրինակ՝ 2.5 թիվը 2.513 թվի մոտավոր արժեքն է մինչև 0.1 ճշտությամբ: Իրոք՝|2.513 – 2.5| = 0.013 < 0.1: