Քառակուսու մակերեսի կախվածությունը կողմից և խորանարդի ծավալի կախվածությունը կողից այնպիսի ֆունկցիաների օրինակներ են, որոնք տրվում են y = x² և y = x³ տեսքի բանաձևերով:
Կառուցենք y = x² ֆունկցիայի գրաֆիկը: Կազմենք x-ի և y-ի համապատասխան արժեքների մի աղյուսակ.

Կառուցենք այն կետերը, որոնց կոորդինատները նշված են աղյուսակում:
Կոորդինատների սկզբնակետի մոտակայքում գրաֆիկն ավելի ճշգրիտ կառուցելու համար հաշվենք ֆունկցիայի ևս մի քանի արժեք.

Աղյուսակից երևում է, որ կոորդինատների սկզբնակետի մոտակայքում ֆունկցիայի գրաֆիկը գրեթե ձուլվում է x առանցքի հետ:
Նշված կետերով տանենք մի սահուն գիծ: Կստանանք y = x² ֆունկցիայի գրաֆիկը:

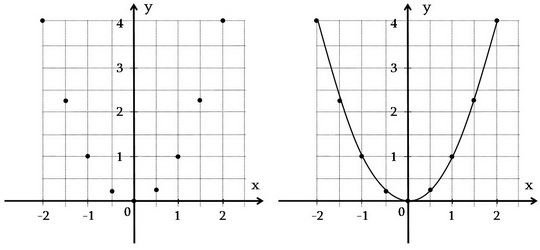Պարզ է, որ այդ գրաֆիկը y առանցքի աջ և ձախ մասերում անսահմանափակորեն շարունակվում է դեպի վեր:
y = x² ֆունկցիայի գրաֆիկն անվանում են պարաբոլ:
Պարզաբանենք y = x² ֆունկցիայի մի քանի հատկություն:
1) Եթե x = 0, ապա y = 0: Այդ պատճառով ֆունկցիայի գրաֆիկն անցնում է կոորդինատների սկզբնակետով:
2) Եթե x ≠ 0, ապա y > 0: Իրոք, զրոյից տարբեր ցանկացած թվի քառակուսին դրական է: Ուստի ֆունկցիայի գրաֆիկի բոլոր կետերը՝ բացի (0, 0) կետից գտնվում են x առանցքից վեր:
3) x-ի հակադիր արժեքներին համապատասխանում է y-ի միևնույն արժեքը: Դա հետևում է այն բանից, որ (-x)² = x² ցանկացած x-ի դեպքում: Նշանակում է, գրաֆիկի այն կետերըորոնք ունեն հակադիր աբսցիսներ, համաչափ են y առանցքի նկատմամբ:
Այժմ կառուցենք y = x³ ֆունկցիայի գրաֆիկը: Կազմենք x-ի և y-ի համապատասխան արժեքները՝ y-ի արժեքները կլորացնելով մինչև հարյուրերորդականներ.

Կառուցենք այն կետերը, որոնց կոորդինատները նշված են աղյուսակում:
Նշված կետերով տանենք սահուն գիծ: Կստանանք y = x³ ֆունկցիայի գրաֆիկը:

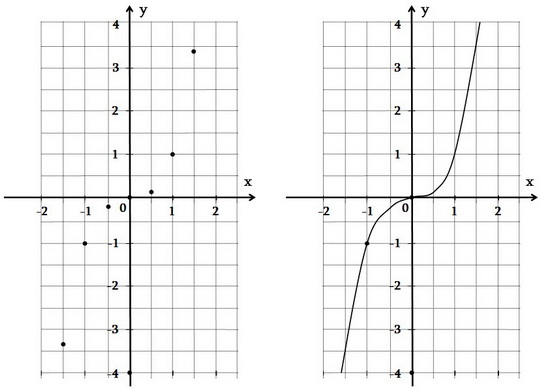Պարզ է, որ այդ գրաֆիկը անսահմանափակորեն շարունակվում է վերև y առանցքից աջ և ներքև՝ y առանցքից ձախ:
Նշենք, որ կոորդինատների սկզբնակետի մոտակայքում ֆունկցիայի գրաֆիկը գրեթե ձուլվում է x առանցքին (եթե x = 0.1, ապա y = 0.001, եթե x = 0.2, ապա y = 0.008, եթե x = 0.3, ապա y = 0.027):
Պարզաբանենք y = x³ ֆունկցիայի մի քանի հատկություն:
1) Եթե x = 0, ապա y = 0: Այդ պատճառով ֆունկցիայի գրաֆիկն անցնում է կոորդինատների սկզբնակետով:
2) Եթե x > 0, ապա y > 0, եթե x < 0, ապա y < 0: Իրոք՝ դրական թվի խորանարդը դրական թիվ է, իսկ բացասական թվի խորանարդը՝ բացասական: Նշանակում է ֆունկցիայի գրաֆիկը գտնվում է առաջին և երրորդ կոորդինատային քառորդներում:
3) x-ի հակադիր արժեքներին համապատասխանում են y-ի հակադիր արժեքներ: Դա հետևում է այն բանից, որ x-ի ցանկացած արժեքի դեպքում ճիշտ է (-x³) = -x³ հավասարությունը: Ուստի՝ գրաֆիկի այն կետերը, որոնք ունեն հակադիր աբսցիսներ, համաչափ են տեղադրված կոորդինատների սկզբնակետի նկատմամբ: