a² * a³ արտահայտությունը նույն հիմքով երկու աստիճանների արտադրյալ է: Այդ արտադրյալը հնարավոր է գրել նույն հիմքն ունեցող աստիճանի տեսքով.a² * a³ = (a * a) * (a * a * a) = a * a * a * a * a = a⁵:Նշանակում է՝a² * ³ = a^{2 + 3}:Մենք տեսնում ենք, որ a² * a³ արտադրյալը հավասար է մի աստիճանի, որի հիմքը նույն a-n է, իսկ ցուցիչը հավասար է բազմապատկվող աստիճանների ցուցիչների գումարին: Նույն հատկությունն ունի միևնույն հիմքերով ցանկացած աստիճանների արտադրյալ:
Ցանկացած a թվի և կամայական բնական m և n թվերի համարa^m * aⁿ = a^{m + n}Ապացուցելու համար օգտագործենք աստիճանի սահմանումը և բազմապատկման հատկությունները: a^m * aⁿ արտահայտությունը նախ ներկայացնենք այնպիսի բազմապատկիչների արտադրյալի տեսքով, որոնցից յուրաքանչյուրը հավասար է a-ի, այնուհետև աստիճանի տեսքով՝

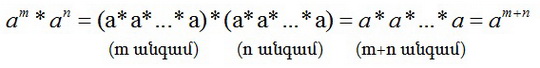Այսպիսով՝a^m * aⁿ = a^m+n:Ապացուցված հավասարությամբ արտահայտվում է աստիճանի հիմնական հատկությունը: Երեք և ավելի աստիճանների արտադրյալը նույնպես օժտված է այդ հատկությամբ: Օրինակ՝a^m * aⁿ * a^k = a^m+n+k:Աստիճանի հիմնական հատկությունից հետևում է աստիճանների բազմապատկման կանոնը. Նույն հիմքերով աստիճանները բազմապատկելիս հիմքը թողնում են անփոփոխ, իսկ աստիճանացույցերը գումարում:
Բերենք մի քանի օրինակ.x⁸ * x⁷ = x¹⁵, y * y⁵ = y¹ * y⁵ = y⁶, b² * b⁴ * b³ = b²⁺⁴⁺³ = b⁹:a⁷ : a³ արտահայտությունը նույն հիմքերով երկու աստիճանների քանորդ է: Այդ քանորդը a ≠ 0 դեպքում հնարավոր է ներկայացնել նույն հիմքով աստիճանի տեսքով: Իրոք՝ քանի որ a³ * a⁴ = a⁷, ապա ըստ քանորդի սահմանման՝a⁷ : a³ = a⁴, այսինքն՝ a⁷ : a³ = a^7-3:Մենք տեսնում ենք, որ a⁷ : a³ քանորդը հավասար է մի աստիճանի, որի հիմքը նույն a-ն է, իսկ աստիճանը հավասար է բաժանելիի և բաժանարարի ցուցիչների տարբերությանը:
Նույն հատկությամբ է օժտված զրոյից տարբեր նույն հիմքն ունեցող կամայական աստիճանների քանորդը, որի մեջ բաժանելիի աստիճանացույցը մեծ է աստիճանացույցից:
Ցանկացած a ≠ 0 թվի և կամայակսն m և n բնական թվերի համար, որտեղ m > na^m : aⁿ = a^m-n:a^m : aⁿ= a^m-n հավասարությունը կապացուցվի, եթե ցույց տանք, որ a^m-n-ի և aⁿ-ի արտադրյալը հավասար է a^m:
a^m-n * aⁿ արտադրյալի նկատմամբ կիրառելով աստիճանի հիմնական հատկությունը կստանանք՝a^m-n * aⁿ = a^(m-n)+n = a^m-n+n = a^m:Ուստի ըստ քանորդի սահմանման՝a^m : aⁿ = a^m-n:Ապացուցված այս հատկությունից հետևում է աստիճանների բաժանման կանոնը. նույն հիմքերով աստիճանները բաժանելիս հիմքը թողնում են անփոփոխ, իսկ բաժանելիի աստիճանացույցից հանում են բաժանարարի աստիճանացույցը:
Բերենք մի քանի օրինակ,c¹⁰ : c² = c^10-2 = c⁸, p⁷ : p = p⁷ : p¹ = p^7-1 = p⁶:Մենք արտածեցինք a^m-ը aⁿ-ի բաժանելու կանոնը այն դեպքի համար, երբ m > n: Եթե այդ կանոնը կիրառենք a^m : aⁿ քանորդի նկատմամբ, ապա կստացվի՝aⁿ : aⁿ = a^n-n = a⁰:Զրո ցուցիչով աստիճանը չի սահմանվել: Քանի որ ամեն մի a ≠ 0 դեպքում և ցանկացած բնական n-ի համար՝aⁿ : aⁿ = 1,ապա համարում են, որ a ≠ 0 դեպքում՝a⁰ = 1:Սահմանում: Զրոյից տարբեր a թվի զրո ցուցիչով աստիճանը հավասար է մեկի:
Օրինակ՝ 2⁰ = 1, (-3.5)⁰ = 1: 0⁰ արտահայտությունը իմաստ չունի: Այժմ՝ զրո ցուցիչով աստիճանը սահմանելուց հետո, կարող ենք a^m * aⁿ = a^m+n բանաձևը (a ≠ 0 դեպքում) կիրառել նաև այն դեպքերում, երբ m = 0 կամ n = 0: a^m: aⁿ = a^m-n բանաձևը, երբ a ≠ 0, կարելի է կիրառել ցանկացած ամբողջ ոչ բացասական m և n թվերի դեպքում, որոնք բավարարում են m ≥ n պայմանին: