Երկու գծային ֆունկցիաների գրաֆիկները ուղիղներ են, որոնք կամ հատվում են, կամ զուգահեռ են:

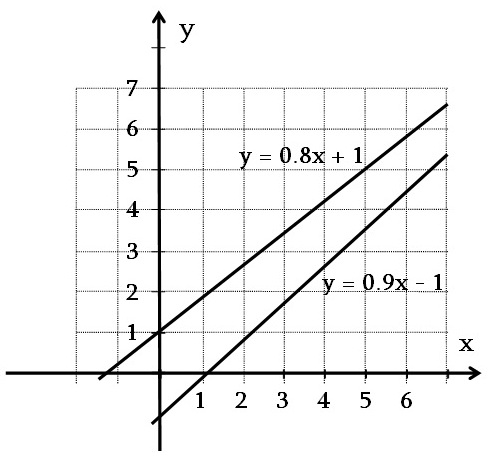Դիտարկենք, օրինակ, y = 0.9x -1 և y = 0.8x + 1 բանաձևերով տրված ֆունկցիաների գրաֆիկները, որոնց մեջ x-ի գործակիցները տարբեր են: Պարզենք, թե արդյոք հատվո՞ւմ են այդ գրաֆիկները:
Գրաֆիկների հատում նշանակում է, որ նրանք ունեն ընդհանուր կետ: Այդ դեպքում կգտնվի x-ի այնպիսի արժեք, որին կհամապատասխանի նույն y-ը երկու ֆունկցիաների համար էլ: x-ի այդ արժեքը գտնելու համար պետք է լուծել 0.9x - 1 = 0.8x + 1 հավասարումը:0.9x - 0.8x = 1 + 1,
0.1x = 2, x = 20:Երբ x = 20, y = 0.9x - 1 և y = 0.8x + 1 երկու ֆունկցիաներն էլ ընդունում են միևնույն արժեքը՝ 17: (20, 17) կետը պատկանում է ինչպես մեկ, այնպես էլ մյուս գրաֆիկին: Այդ կետը միակն է: Ուստի՝ y = 0.9x - 1 և y = 0.8x + 1 ֆունկցիաների գրաֆիկներ հանդիսացող ուղիղները հատվում են:

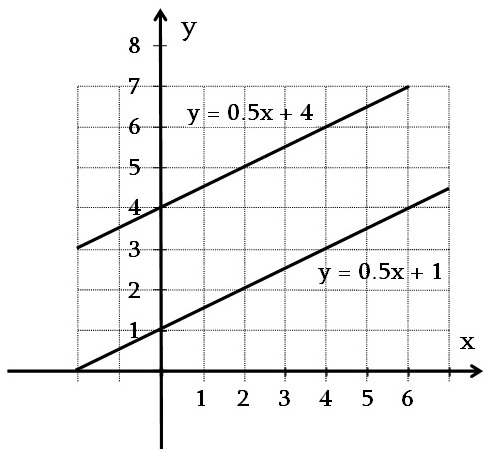Այժմ դիտարկենք y = 0.5x + 4 և y = 0.5x + 1 բանաձևերով տրված գծային ֆունկցիաները, որոնց մեջ x-ի գործակիցները նույնն են: Պարզելու համար՝ հատվում են այդ գրաֆիկները, թե ոչ, պետք է լուծել 0.5x + 4 = 0.5x + 1 հավասարումը: Քանի որ այդ հավասարումն արմատներ չունի, ապա y = 0.5x + 4 և y = 0.5x + 1 ֆունկցիաների գրաֆիկներ հանդիսացող ուղիղները ընդհանուր կետեր չունեն, այսինքն զուգահեռ են:
Ընդհանրապես՝ y = kx + b տեսքի բանաձևերով տրված երկու գծային ֆունկցիաների գրաֆիկները հատվում են, եթե x-ի գործակիցները տարբեր են, և զուգահեռ են, եթե x-ի գործակիցները նույնն են:
Դա ապացուցենք: Դիցուք y = k₁x + b₁ և y = k₂x + b₂ ֆունկցիաները երկու տարբեր գծային ֆունկցիաներ են: Պարզելու համար, թե ինչ փոխդասավորություն ունեն նրանց գրաֆիկները, դիտարկենք հավասարումը.k₁x + b₁ = k₂x + b₂
k₁x - k₂x = b₂ - b₁
(k₁ - k₂) * x = b₂ - b₁Եթե k₁ ≠ k₂, ապա այդ հավասարումն ունի միակ արմատ: Այդ դեպքում ֆունկցիաների գրաֆիկները հատվում են: Եթե k₁ = k₂ և b₁ ≠ b₂, ապա հավասարումն արմատ չունի: Այդ դեպքում ֆունկցիաների գրաֆիկները զուգահեռ են:

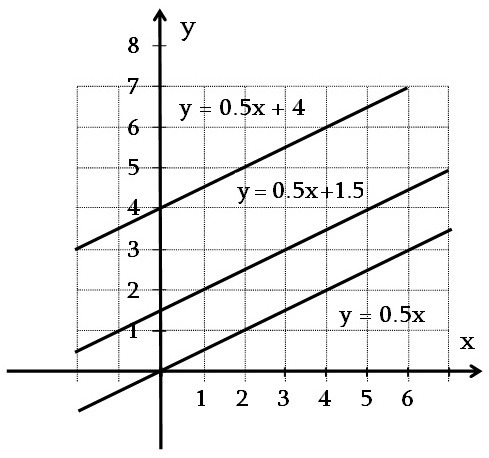Նկարում պատկերված են ուղիղներ, որոնք y = kx + b տեսքի բանաձևերով տրված գծային ֆունկցիաների գրաֆիկներ են, որոնց մեջ x-ի գործակիցները նույնն են, իսկ b-ի արժեքները՝ տարբեր: Այդ բոլոր ուղիղները զուգահեռ են և x առանցքի նկատմամբ թեքված են նույն անկյամբ: Այդ անկյունը կախված է k գործակցից: k թիվն անվանում են y = kx + b ֆունկցիայի գրաֆիկ հանդիսացող ուղիղ անկյան գործակից:
Օգտագործելով ուղիղ անկյան գործակից տերմինը, վերևում ապացուցված հատկությունը կարելի է ձևակորպել այսպես. եթե երկու գծային ֆունկցիաների գրաֆիկներ հանդիսացող ուղիղների անկյունային գործակիցները տարբեր են, ապա այդ ուղիղները հատվում են, իսկ եթե անկյունային գործակիցները նույնն են, ապա ուղիղները զուգահեռ են:

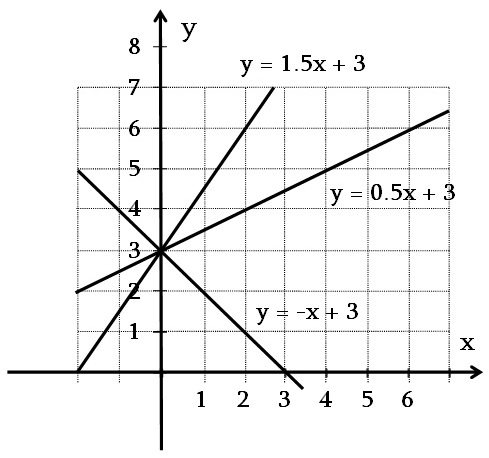y = kx + b բանաձևից հետևում է, որ x = 0 դեպքում y-ի արժեքը հավասար է b-ի: Նշանակում է՝ y = kx + b ֆունկցիայի գրաֆիկը y առանցքը հատում է (0, b) կոորդինատներով կետում: Նկարում պատկերված են ուղիղներ, որոնք y = kx + b տեսքի բանաձևերով տրված ֆունկցիաների գրաֆիկներ են, որտեղ k-երը տարբեր են, իսկ b-ի արժեքները՝ նույնը: Այդ բոլոր ուղիղները հատվում են մեկ կետում՝ որը գտնվում է y առանցքի վրա;