Դիտարկենք ֆունկցիաների օրինակներ:Օրինակ 1: Մայրուղու վրա գտնվում են A և երկու B կետերը, որոնց միջակա հեռավորությունը 20կմ է: Մոտոցիկլավարը դուրս եկավ B կետից և 50կմ/ժ արագությամբ շարժվեց A կետի հակառակ ուղղությամբ: t ժամում մոտոցիկլավարը կանցնի 50t կմ և A-ից հեռու կլինի (50t + 20) կմ: Եթե s տառով նշանակենք A կետից մոտոցիկլավարի հեռավորությունը (կիլոմետրերով), ապա այդ հեռավորության կախվածությունը շարժման ժամանակամիջոցից կարելի է արտահայտել հետևյալ բանաձևով.s = 50t + 20, որտեղ t ≥ 0:Օրինակ 2: Աշակերտը գնել է 30 դրամանոց տետրեր և 150 դրամանոց մի գրիչ: Վճարը կախված է տետրերի թվից: Գնված տետրերի թիվը նշանակենք x, իսկ վճարը (դրամներով) y տառով:
Կստանանք.y = 30x + 150, որտեղ x-ը բնական թիվ է:Երկու օրինակներում էլ մենք հանդիպեցինք այնպիսի ֆունկցիաների, որոնք տրվում են y = kx + b տեսքի բանաձևերով, որտեղ x-ը անկախ փոփոխական է, k-ն և b-ն թվեր են: Այդպիսի ֆունկցիաները կոչվում են գծային:
Սահմանում: Գծային ֆունկցիա կոչվում է այն ֆունկցիան, որը կարելի է տալ y = kx + b տեսքի բանաձևով, որտեղ x-ը անկախ փոփոխական է, իսկ k-ն և b-ն` ինչ-որ թվեր:
Քննարկենք գծային ֆունկցիայի գրաֆիկի հարցը: Ընդ որում կենթադրենք, որ ֆունկցիայի որոշման տիրույթը բաղկացած է բոլոր թվերից: Կառուցենք y = 0.5x - 2 գծային ֆունկցիայի գրաֆիկը: Կազմենք x-ի և y-ի համապատասխան արժեքների աղյուսակը.Կոորդինատային հարթության վրա նշենք այն կետերը, որոնց կոորդինատները նշված են աղյուսակում: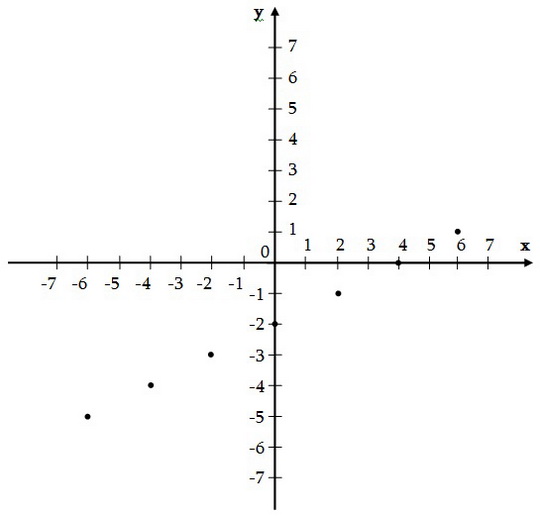Նշված բոլոր կետերը գտնվում են մի ուղղու վրա: Այդ ուղիղը y = 0.5x - 2 գծային ֆունկցիայի գրաֆիկն է: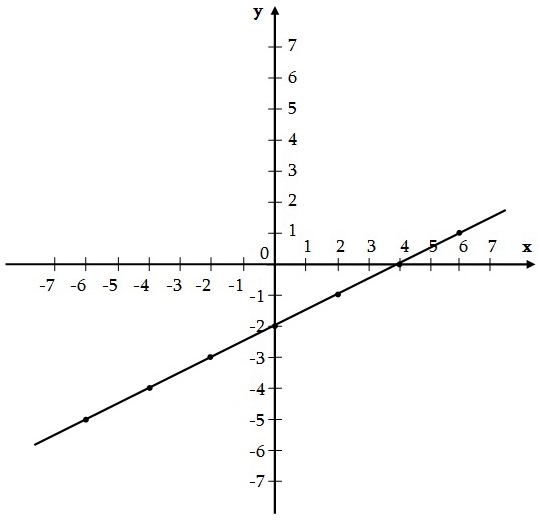Ընդհանրապես` Գծային ֆունկցիայի գրաֆիկը ուղիղ գիծ է:
Գծային ֆունկցիայի գրաֆիկը կառուցելու համար բավական է գտնել գրաֆիկի երկու կետերի կոորդինատները, այդ կետերը նշել կոորդինատային հարթուոյան մեջ և դրանցով տանել ուղիղ:
Օրինակ 3: Կառուցենք y = 2x + 3 ֆունկցիայի գրաֆիկը:
y = 2x + 3 ֆունկցիան գծային է, ուստի նրա գրաֆիկը ուղիղ գիծ է: Օգտագործելով y = 2x + 3 բանաձևը, գտնենք գրաֆիկի երկու կետի կոորդինատները.
եթե x = -2, ապա y = 2 * (-2) + 3 = -1,
եթե x = 1, ապա y = 2 * 1 + 3 = 5:
Նշենք A(-2, -1) և B(1, 5) կետերը: Այդ կետերով տանենք ուղիղ: AB ուղիղը y = 2x + 3 ֆունկցիայի գրաֆիկն է: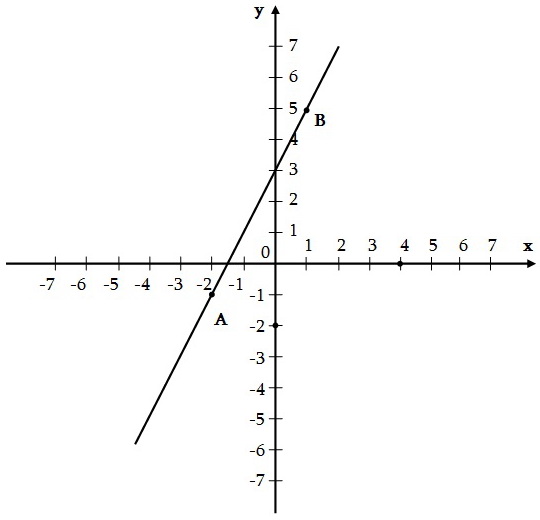k = 0 դեպքում y = kx + b բանաձևը, որով տրվում է գծային ֆունկցիան, ունի y = 0x + b, այսինքն` y = b տեսքը: y = b բանաձևով տրվող գծային ֆունկցիան միևնույն արժեքն է ընդունում ցանկացած x-ի դեպքում:
Օրինակ 4: Կառուցենք y = -2 ֆունկցիայի գրաֆիկը:
x-ի ցանկացած արժեքի համապատասխանում է y-ի միևնույն արժեքը` -2: Նշենք որևէ երկու կետ` -2 օրդինատով. օրինակ` A(0, -2) և B(4, -2), և նրանցով տանենք մի ուղիղ: AB ուղիղը y = -2 գծային ֆունկցիայի գրաֆիկն է: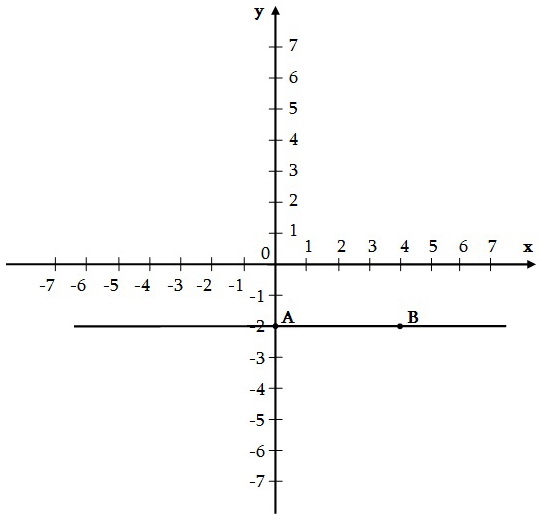Նշենք, որ եթե գծային ֆունկցիայի որոշման տիրույթը բոլոր թվերը չեն, ապա նրա գրաֆիկը ուղիղ համապատասխան մասն է: Օրինակ` դա կարող է լինել կիսաուղիղ կամ հատված: